Exercício

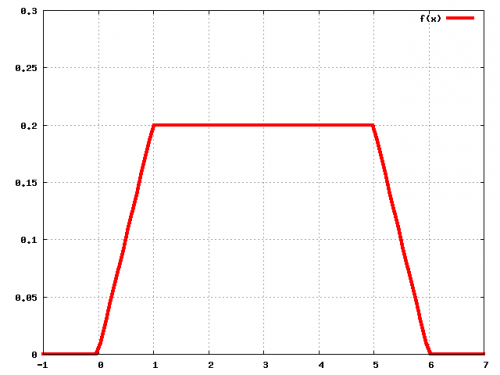
Primeiro o gráfico:

Tem que entender o gráfico, se não fica difícil explicar o resto. Basta calcular o valor da função nos pontos 0,1,5 e 6.

A área da curva tem que ser 1 para ser uma densidade de probabilidade. Tem um triângulo de 0 a 1, um retângulo de 1 a 5 e um triângulo de 5 a 6.

O primeiro triângulo tem área 1*0,2/2=0,1 (base vezes altura/2). O retângulo tem área 4*0,2=0.8 (base x altura) . O terceiro triângulo tem área 1*0.2/2=0.1. Somando tudo dá área=0,1+0,8+0,1=1. Portanto pode ser uma função densidade de probabilidade.

$p(x>1)$ é só somar o retângulo + o último triângulo = 0.8 + 0.1= 0.9

$p(1<x<5)$ é só a área do retângulo: 0.8

$p(0,5<x<5.2)$ este é mais complicado: para $x=0,5$, $f(x)=0.2*0.5=0.1$.

De $x=0,5$ até $x=1$ é um trapézio, e faço a área = base maior + base menor/2 * altura.

Vou fazer o truque de ontem: a altura vai ser de 0,5 a 1=0.5.

A base menor é 0.1 e a base maior é $0,2$. Logo a área vai ser $(0.1+0.2)/2*(0.5)=0.075$.

Agora soma o retângulo todo $(0,8)$.

Falta o trapézio final ($x=5.2$).

Para $x=5.2$, $f(x)=1,2-0.2x=1.2-0.2*5.2=0.16$.

O trapézio vai de $x=5$ até $x=5.2$ (altura$=5.2-5.0=0.2$), com base maior $0.2$ e base menor $0.16$.

A área dá $(0.2-0.16)/2*0.2=0,004$.

A área total é $0.004+0.8+0.075=0.879$.