Como uma mancha cresce

Eu já comentei aqui, o problema do caminho aleatório (Random Walk). Falei no post do O azeite bêbado e fiz algumas simulações com o Processing.js, disponíveis na página do curso de Física Estatística que estou ministrando neste semestre. A experiência que eu quero realizar é medir como o diâmetro de uma mancha de tinta em uma folha de papel varia com o tempo. Vale ressaltar que este probleminha é inspirado em um outro que mostrou que átomos existem, ou comportamentos em mercados de ações, como um gás venenoso se espalha pelo ar, etc.

O que eu fiz foi o seguinte: filmei uma gota de tinta que cai no papel.

Agora eu retiro frames do vídeo, em intervalos regulares. O vídeo foi gravado a 30 fps, com uma câmera digital comum. O problema que eu enfrentei é que eu não quero todos os frames (são 7 segundos de filme, com 30 por segundo seriam 210 para analisar e eu queria por volta 15). Os programas que havia testado ou retiravam todos os frames ou só faziam snapshots de 1 em 1 segundo. A dica para resolver isto foi passada pelo Armando M. Baratti, na lista do Arch Linux. O que devemos fazer pelo ffmpeg é o seguinte: ele só tira frames de 1 em 1s, mas podemos mudar a velocidade do filme. Se repassarmos o filme em 15 fps por segundo, então 0.5s do filme original vai ser 1s do filme repassado. A sintaxe então é simples:

ffmpeg -i mvi_6484.avi -r 10 -ss 00:00:04 -t 00:00:06 extracted_images/images%03d.png

que faz o seguinte: pega o arquivo mvi_6484.avi, a partir do quarto segundo, com duração de seis segundos e tira 10 fotos por segundo. As fotos são salvas no diretório extracted_images, e com um rótulo que indica a ordem do frame. Eu pego cada foto e uso o Gimp para medir o tamanho da mancha. Depois uso o Gnuplot para medir o tamanho em função do número do frame (nem precisa saber quanto tempo em unidades tradicionais como minuto ou segundo). O resultado está no gráfico abaixo do tamanho em pixels versus o índice do frame

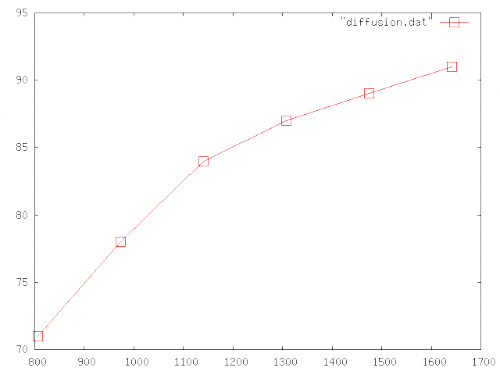
Observe que a gota não cresce com velocidade constante, mas é mais lenta à medida que o tempo passa. Na verdade, o raio da gota cresce com a raiz quadrada do tempo (como mostrado por Einstein em 1905). Eu não vou dar detalhes aqui pois isto é um trabalho para os estudantes da disciplina :) . Prometo que depois eu conto o resto.