Encontrada a equação para a fita de Möbius

Em matemática, uma superfície é dita não-orientável se você puder caminhar sobre ela e ao voltar ao ponto original, você está em uma imagem refletida da superfície. Embora seja meio complicado de entender em palavras, basta mostrar a superfície não orientável mais conhecida: a fita de Möbius (como vista pelo fantástico M.C.Escher):

Siga o caminho das formigas e você entenderá o que eu quero dizer no parágrafo acima: a formiga que começa passando “por fora” da faixa, logo estará “por dentro” dela O que há de novo no problema é que finalmente foi encontrada a equação para a solução da faixa de Möbius: Eugene Starostin e G. H. M. Van der Heijden do University College of London, resolveram as equações de Euler-Lagrange e mostraram porque é fácil montar uma faixa de largura estreita mas é complicado montar uma faixa mais larga (o sistema acaba virando um triângulo, igual ao símbolo internacional para reciclagem

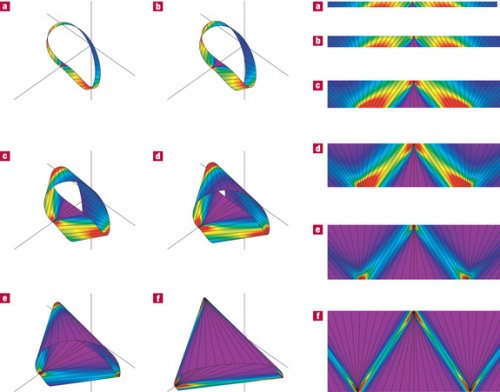
As cores no gráfico acima, indicam a força a que está sujeita cada região da fita.

A solução deste problema pode ter importantes aplicações para o empacotamento de proteínas e macro-moléculas e até explicar porque os fios de telefone convencional às vezes se enroscam à direita e outras, à esquerda.