Considere uma partícula de massa movendo-se em um plano sob a ação de uma força atrativa , dirigida à origem. Determine as equações de movimento
Determine as equações de movimento de uma máquina dupla de Atwood.
Escreve a Lagrangiana de um oscilador harmônico simples e obtenha uma expressão para o período.
Uma partícula de massa desliza em um plano inclinado de massa , que faz um ângulo com a horizontal. O plano está sobre uma superfície plana e não há atrito entre o plano e esta superfície. Determine as acelerações do bloco e do plano.
Determine as equações de Lagrange para um pêndulo duplo, de comprimentos e e massas e . Considere apenas pequenas oscilações.
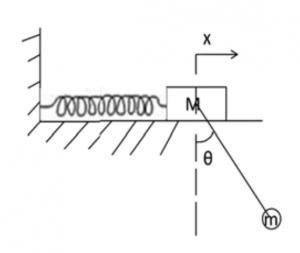
Um pêndulo simples de comprimento e massa está conectado a um bloco de massa , ligado a uma mola de constante elástica (Figura 1). Determine as equações de movimento.
Escreva a Lagrangiana do sistema apresentado na figura 2 abaixo e encontre as equações de movimento (as massas são iguais):
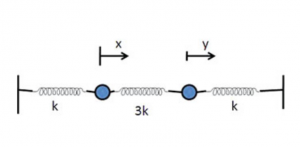
Três partículas com massas respectivamente são conectadas por duas molas de constante elástica . Encontre os modos normais de movimento e suas frequências associadas.
Uma partícula de massa desliza em um buraco semiesférico, mas ainda em um plano vertical (Figura 3). Escreva a Lagrangiana e as equações de movimento, considerando que o bloco não se move
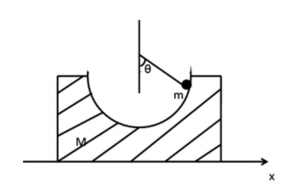
Considere o sistema anterior, mas agora com o bloco podendo se mover em uma superfície sem atrito, ao longo da direção . Escreva a Lagrangiana e as equações de movimento. Depois, considere pequenos deslocamentos e que , encontre o período de oscilação da partícula.



